Soal 30
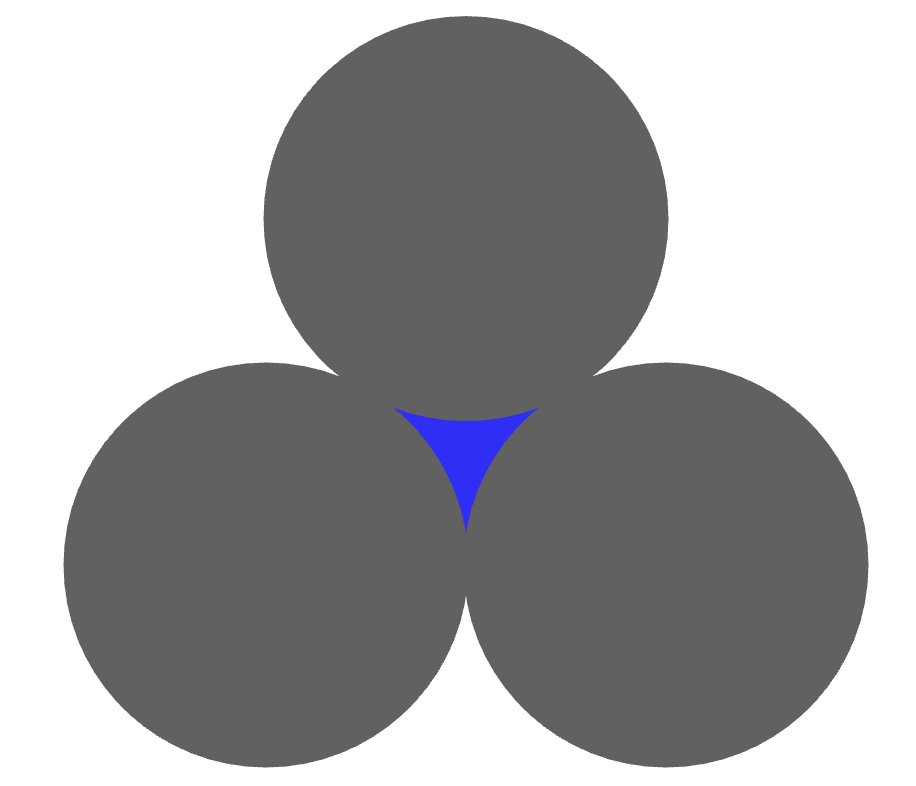
Perhatikan gambar di atas
Tiga buah lingkaran identik dengan jari-jari $r$ saling bersinggungan sedemikian sehingga menyisakan area kosong yang berwarna biru
Nyatakan luas area biru dalam $r$
Solusi
Misalkan titik pusat lingkaran adalah $A$, $B$ dan $C$ dengan jari-jari $r$ dan misalkan titik singgung adalah $P$, $Q$ dan $R$
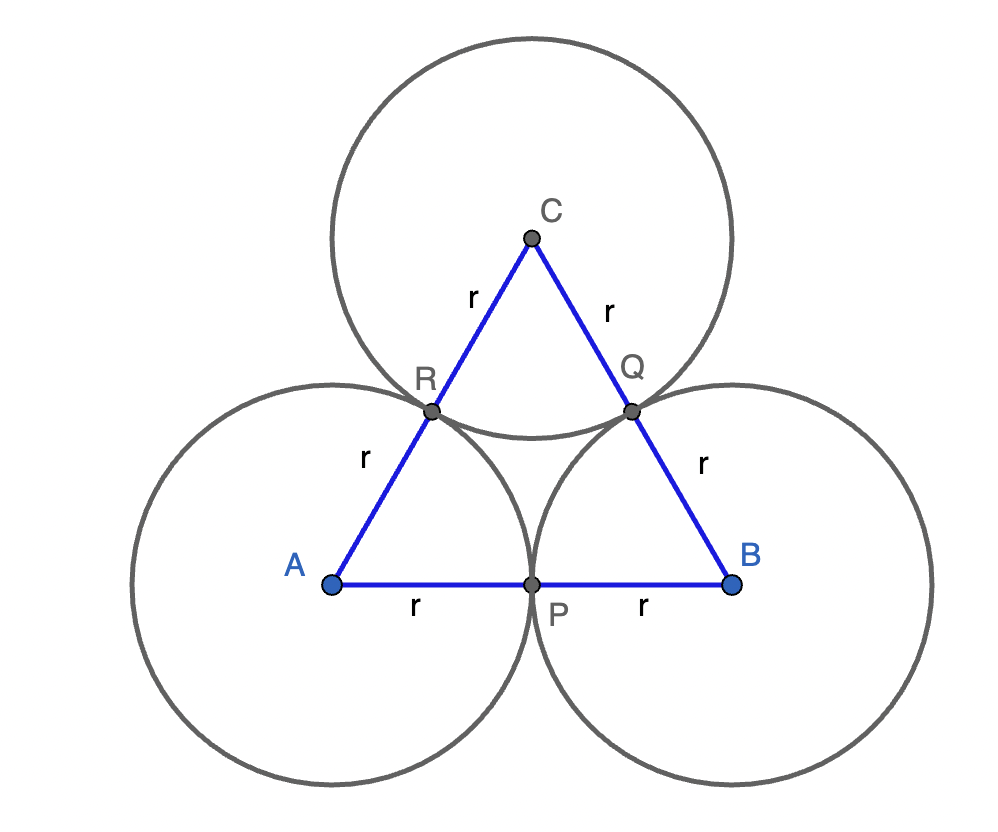
Cukup jelas bahwa $\triangle{ABC}$ adalah segitiga sama sisi. Luasnya adalah $r^2\sqrt{3}$
Karena sama sisi, maka $\angle{PAR}$ adalah $60°$
Karena sudutnya $60°$, maka luas juring $PAR$ adalah $\large{\frac{1}{6}}\pi r^2$
Dengan demikian, luas area biru adalah $r^2\sqrt{3}-\large{\frac{3}{6}}\pi r^2=(\sqrt{3}-\large{\frac{\pi}{2}})r^2$