Soal 31

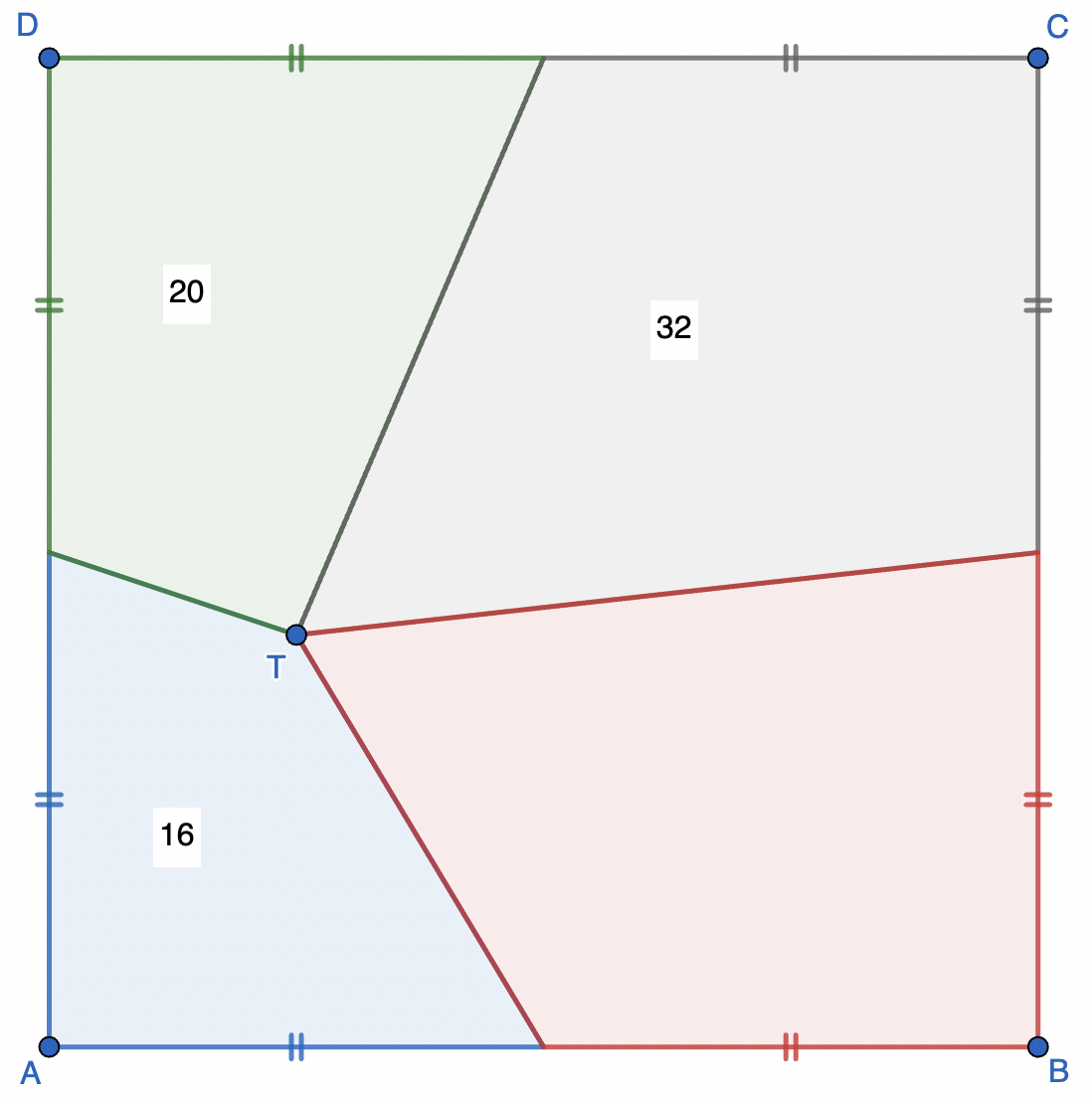
Perhatikan gambar di atas
Sebuah titik $T$ terletak di dalam sebuah persegi $ABCD$ sedemikian sehingga garis yang ditarik dari $T$ menuju titik tengah setiap sisi persegi menciptakan empat buah poligon, yaitu

• poligon biru dengan luas 16
• poligon hijau dengan luas 20
• poligon kelabu dengan luas 32
• poligon merah

Solusi

Tarik garis bantu dari titik sudut persegi ke titik $T$

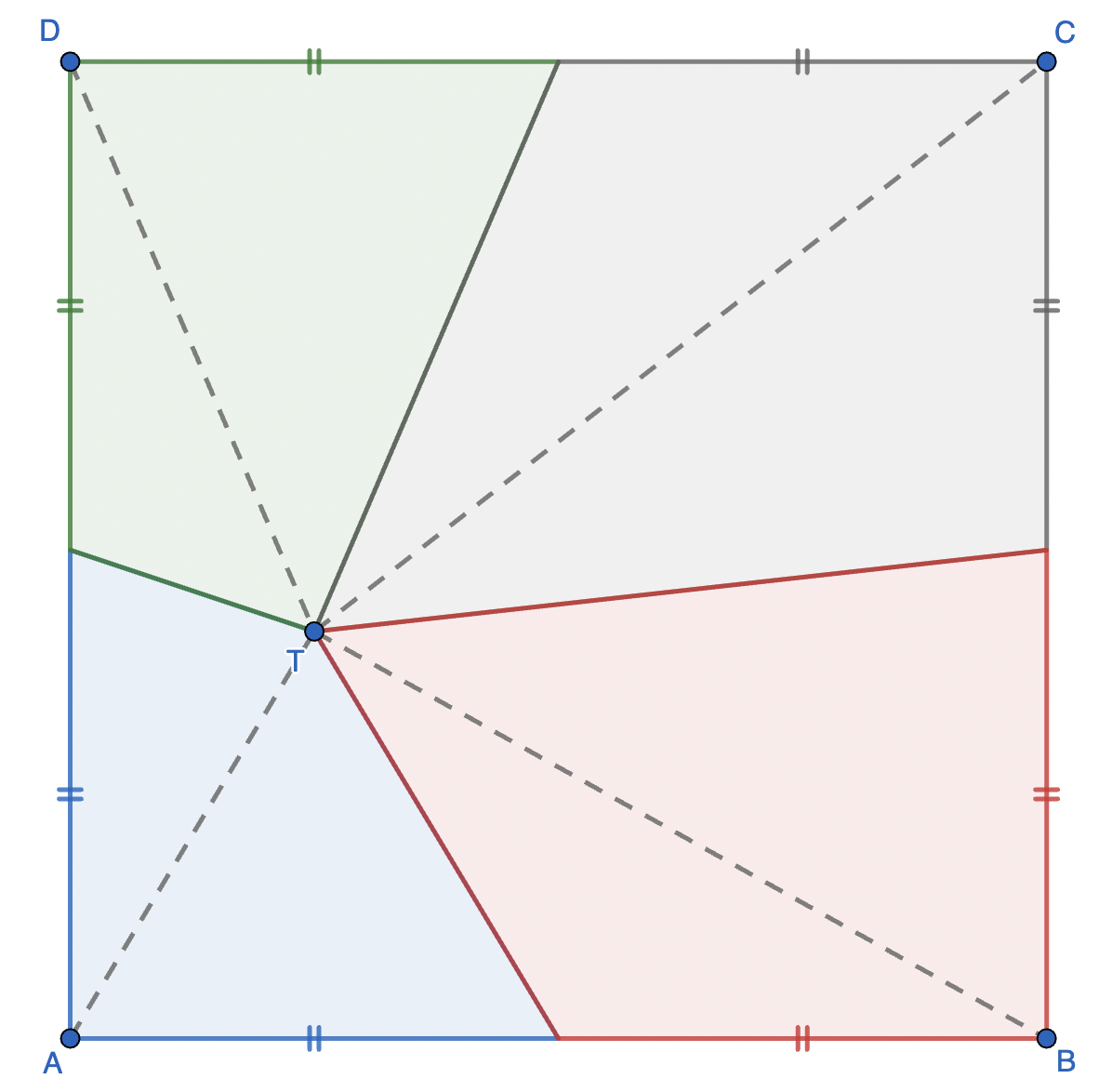
Ingat bahwa rasio luas segitiga dengan tinggi yang sama adalah sama dengan rasio panjang alasnya, yaitu

$\large{\frac{\text{luas }\triangle{AET}}{\text{luas }\triangle{BET}}}=\frac{AE}{BE}$

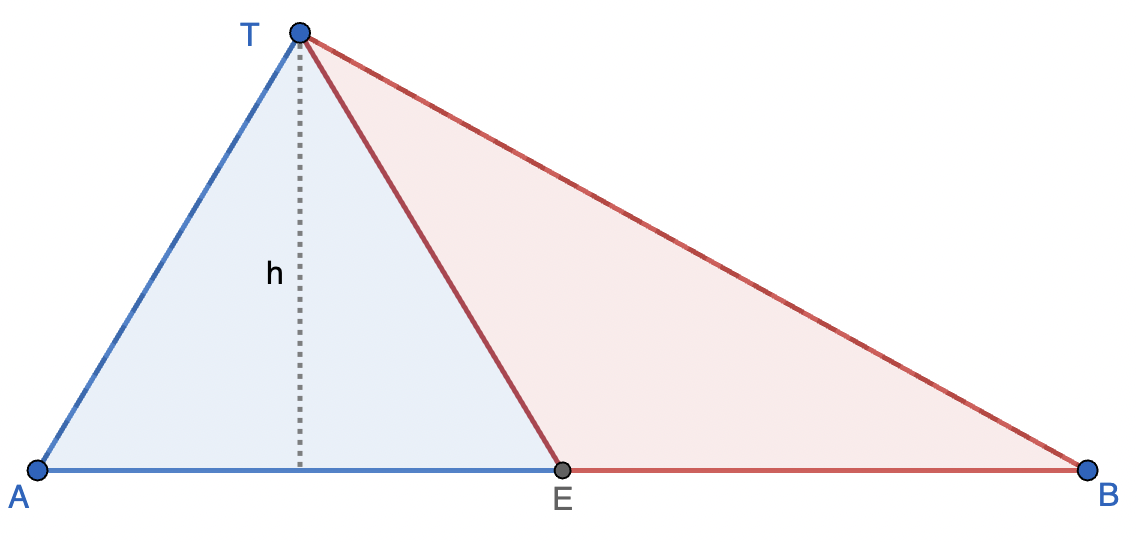
Dari konsep di atas, kita bisa tahu luas segitiga-segitiga di atas

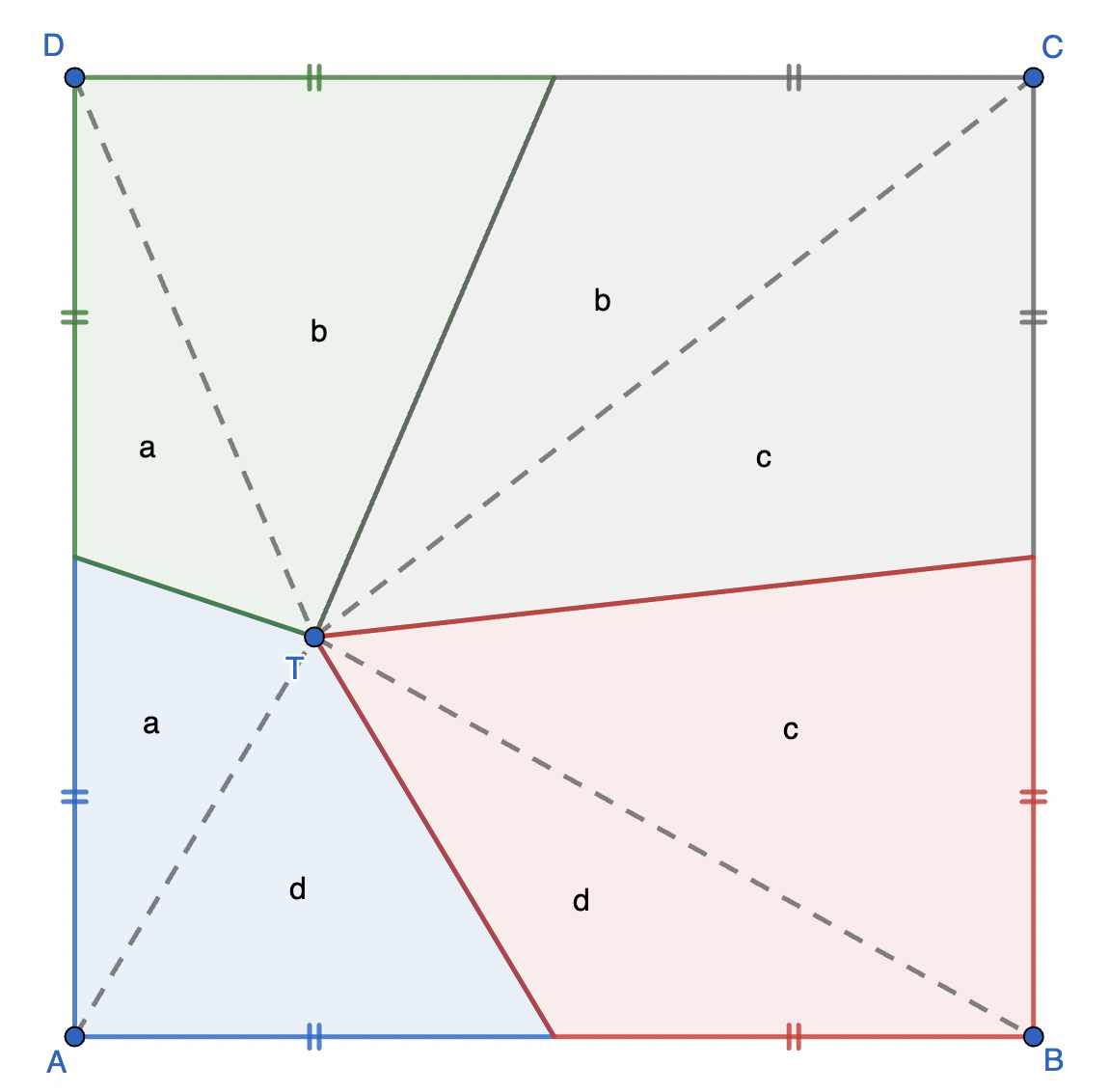
Secara visual, kita tahu:
$\text{luas biru} + \text{luas kelabu} = \text{luas hijau} + \text{luas merah}$
Kita dapat $\text{luas merah}=28$

Misalkan panjang sisi persegi adalah $2s$, kita dapat $s=2\sqrt{6}$

Misalkan koordinat $T$ adalah $(x,y)$

Persamaan 1:
$a + d = 16$
$\frac{1}{2}sx + \frac{1}{2}sy = 16$

Persamaan 2:
$a + b = 20$
$\frac{1}{2}sx + \frac{1}{2}s(2s-y) = 20$
$\frac{1}{2}sx - \frac{1}{2}sy + s^2 = 20$

Dari persamaan (1) dan (2) kita dapat koordinat $T$ adalah $(\sqrt{6},\frac{10}{\sqrt{6}})$