Soal 31
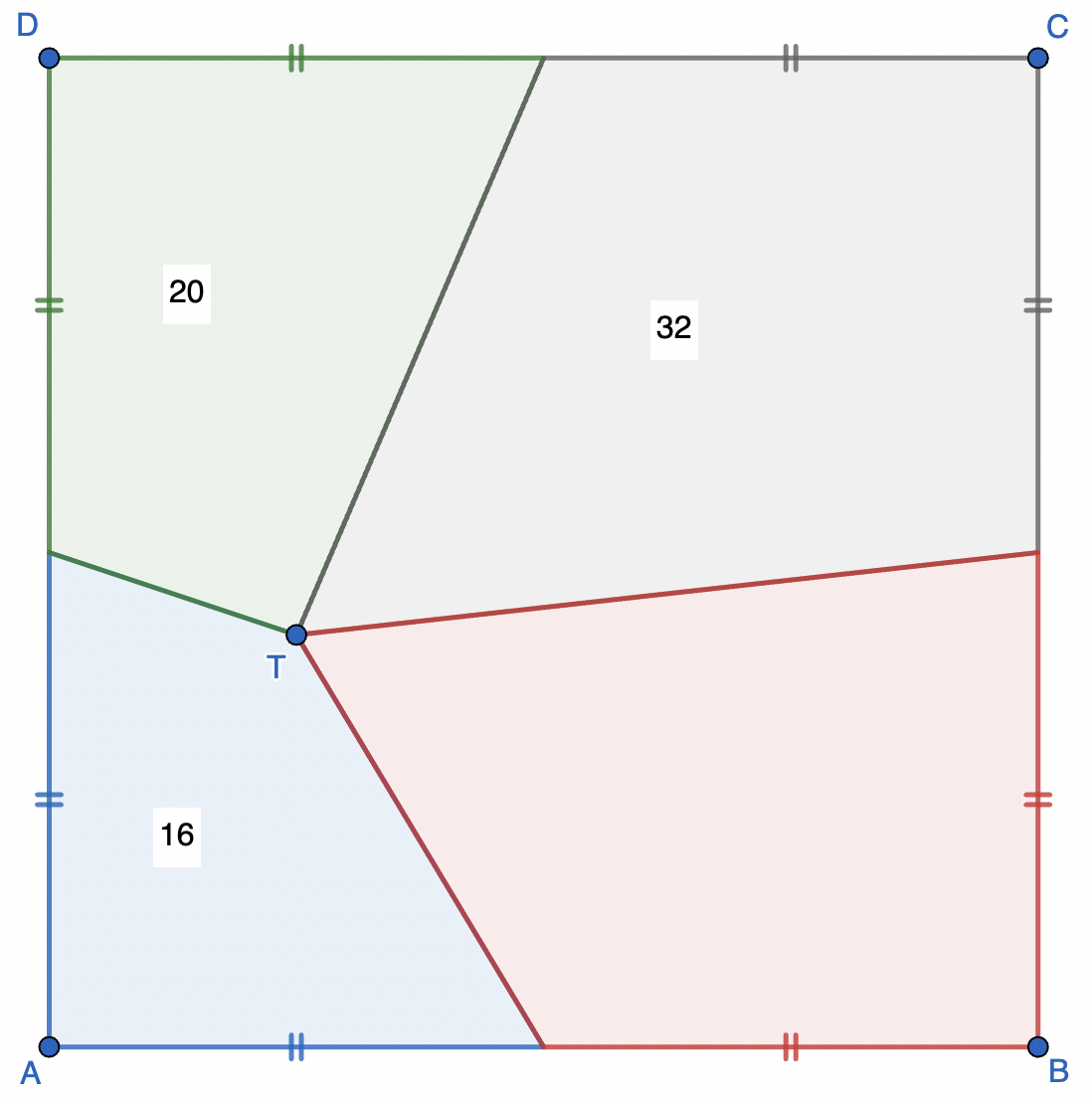
Perhatikan gambar di atas
Sebuah titik $T$ terletak di dalam sebuah persegi $ABCD$ sedemikian sehingga garis yang ditarik dari $T$ menuju titik tengah setiap sisi persegi menciptakan empat buah poligon, yaitu
- poligon biru dengan luas 16
- poligon hijau dengan luas 20
- poligon kelabu dengan luas 32
- poligon merah
b) Jika kita asumsikan $A$ berada di koordinat $(0,0)$, carilah koordinat $T$
Soal 29
Misalkan $p,q \in \mathbb{N}$ sedemikian sehingga
$\large{\frac{p}{q}=1-\frac{1}{2}+\frac{1}{3}-...+\frac{1}{1319}}$
Buktikan bahwa $p$ habis dibagi $1979$
Asumsikan $\large{\frac{p}{q}}$ sudah di dalam bentuk yang paling sederhana
Sumber: International Math Olympiad 1979 - Problem 1
Rumus abc
Buktikan akar-akar dari persamaan kuadrat $ax^2+bx+c=0$ adalah $\large{\frac{-b \pm \sqrt{b^2-4ac}} {2a}}$
Dimana $a \neq 0$